विमान पर आंकड़े प्रदर्शित करना (परिभाषा)

2024 लेखक: Leah Sherlock | [email protected]. अंतिम बार संशोधित: 2023-12-17 05:37

शीट, कैनवास और किसी भी अन्य सतह पर विभिन्न आकृतियों को सही ढंग से प्रदर्शित करने की क्षमता काफी महत्वपूर्ण कौशल है। और सबसे बढ़कर, यह कला के लोगों के लिए महत्वपूर्ण है: चित्रकार, मूर्तिकार, ग्राफिक कलाकार, डिजाइनर (आंतरिक स्थान और स्थापत्य वातावरण के), और विज्ञान के लोगों के लिए: गणितज्ञ, भौतिक विज्ञानी, डिजाइनर, आविष्कारक।

लेकिन इन क्षेत्रों से दूर रहने वाले व्यक्ति के लिए यह भी महत्वपूर्ण है कि वह अपने आसपास की दुनिया को सही ढंग से देखना और प्रदर्शित करना सीखे। यह इसकी सभी बहुमुखी प्रतिभा को और अधिक गहराई से समझने में मदद करता है। यदि आपके पास इसे सही तरीके से करने का पर्याप्त विचार नहीं है, तो आप किसी भी आविष्कार के प्रोजेक्ट, चित्र या ड्राइंग में सफल नहीं होंगे। अर्थात्, यह कौशल सरल, रोज़मर्रा के कार्यों को हल करने और वैश्विक, सार्वभौमिक महत्व वाले लोगों के लिए दोनों के लिए महत्वपूर्ण है।

थोड़ा सा इतिहास

प्राचीन काल से, लोगों ने अपने आस-पास जो कुछ देखा, उसे चित्रित करने का प्रयास किया है: अन्य लोग, उस समय की कुछ आदिम इमारतें, पौधों और जानवरों की एक अद्भुत सुंदर दुनिया, राजसी पहाड़, और साधारण चीजें, घरेलू सामान। यानी दुनिया अपनी सारी विविधता और भव्यता में।

लेकिन तब भी उन्हें इस बात का अंदाजा नहीं था कि यह कैसे सही और सक्षम तरीके से किया जा सकता है, ताकि एक विमान पर विभिन्न त्रि-आयामी वस्तुओं का प्रदर्शन वास्तव में यथार्थवादी, जीवंत हो। उस व्यक्ति के पास प्रासंगिक ज्ञान नहीं था और, इसके अलावा, कोई विशेष कौशल नहीं था, शायद सबसे प्राथमिक कौशल को छोड़कर।

पहले के सूत्रों में कहा गया है कि दुनिया की पहली पेंटिंग में सिर्फ एक लाइन थी जो दीवार पर सूर्य द्वारा डाली गई किसी व्यक्ति की छाया के साथ जाती थी। यानी प्रकृति ने ही सुझाव दिया कि इस मुद्दे के सही समाधान की तलाश में किस दिशा में बढ़ना उचित है।

और इस सवाल ने उस समय के आदमी को इस कारण से भी चिंतित किया: वह न केवल विशाल जीवित सिल्हूट की प्रशंसा करना चाहता था, मूल, इसलिए बोलने के लिए, बल्कि एक विमान पर एक स्थानिक वस्तु को पकड़ने की मांग की। और उसने ऐसा इसलिए किया ताकि इस तरह से वह या तो अपने घर को सजा सके या अपने पवित्र स्थान को सजा सके, या अपने साथ एक तस्वीर के साथ एक बंडल ले जा सके और उसे किसी भी दूरी पर ले जा सके।

पैटर्न ज्यामिति

और आप जो कुछ भी कहते हैं, लेकिन साल बीत गए, सदियां बीत गईं, और किसी तरह, जैसे-जैसे सभ्यता विकसित हुई, लोगों ने धीरे-धीरे दो-आयामी अंतरिक्ष में जटिल आकृतियों को प्रदर्शित करना सीखा, यानी एक विमान पर। केवल अब चित्रित वस्तुओं के आकार और अनुपात की सटीकता बहुत अनुमानित लगने लगी थी।

लेकिन यह सवाल कि विमान पर आकृति का प्रदर्शन कितना सही है और वे मूल वस्तुओं के आयतन से कितना मेल खाते हैं, एक बार बहुत प्रासंगिक हो गया। किसी तरह, एक नया विज्ञान कहा जाता हैज्यामिति। अधिक सटीक रूप से, इसका खंड वर्णनात्मक ज्यामिति है।

यहाँ वह सिर्फ आकृतियों और विमानों, रेखाओं और बिंदुओं का अध्ययन कर रही है, साथ ही एक दूसरे के सापेक्ष उनके संबंध - त्रि-आयामी और द्वि-आयामी अंतरिक्ष दोनों में।

रूपांतरण के तरीके

दृश्य कला में एक महत्वपूर्ण विशेषता छवि तल पर आकृतियों का प्रदर्शन है। आखिरकार, वास्तव में, यह द्वि-आयामीता में त्रि-आयामी स्थानिक वस्तुओं का कब्जा है। अर्थात्: कॉम्प्लेक्स को एक साधारण में परिवर्तित किया जाना चाहिए, यानी एक वस्तु जिसकी लंबाई, चौड़ाई, ऊंचाई है, उसे एक विमान में स्थानांतरित किया जाना चाहिए।

और वर्णनात्मक ज्यामिति कुछ तरीकों की बदौलत ऐसे "संक्रमण" करती है। उनमें से कुल मिलाकर लगभग छह हैं। यहां तीन मुख्य और दुनिया भर में सबसे लोकप्रिय हैं:

• परिप्रेक्ष्य (जब चित्रित वस्तु को अंतरिक्ष में हटा दिया जाता है);
• ऑर्थोगोनल प्रोजेक्शन (समानांतर में प्रक्षेपण, जहां किरणें समतल पर लंबवत होती हैं);
• तिरछा प्रक्षेपण (समानांतर में प्रक्षेपण, जहां किरणें समतल के सापेक्ष झुकी होती हैं)।

चित्रित वस्तु एक्सोनोमेट्रिक प्रोजेक्शन (जिसमें ऑर्थोगोनल और तिरछा शामिल है) में काफी स्पष्ट रूप से दिखाई देता है। लेकिन इसे सबसे स्पष्ट और सही मायने में तब पेश किया जाता है जब इसे परिप्रेक्ष्य में दिखाया जाता है। और यह उपरोक्त तरीके हैं जो बड़े पैमाने पर इस सवाल को हल करते हैं कि एक विमान पर आंकड़े कैसे प्रदर्शित करें।

परिप्रेक्ष्य

छवि के अन्य तरीकों में परिप्रेक्ष्य सबसे सम्मानजनक स्थान लेता है। क्योंकि इंसान की आँखएक कैमरा लेंस की तरह, यह आसपास के स्थान को भी इसी तरह से देखता है। जो चीजें प्रेक्षक से अधिक दूर होती हैं वे आकार में छोटी और कभी-कभी निकट होने की तुलना में बहुत छोटी दिखाई देती हैं।

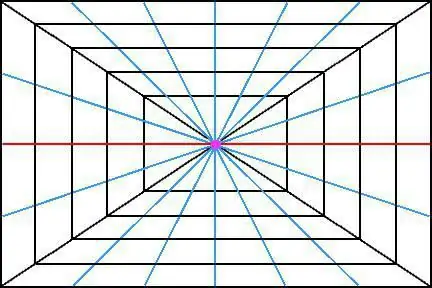
उदाहरण के लिए, अंतरिक्ष में एक घन का प्रतिबिम्ब लें। यदि, वास्तव में, इसके सभी किनारे एक दूसरे के समानांतर हैं, तो जब आप इस वस्तु को दूर से देखते हैं, तो ऐसा लग सकता है कि किनारे एक बिंदु पर अभिसरण (या अभिसरण) होना चाहिए। और, जो सबसे दिलचस्प है, उन्हें न केवल एक बिंदु पर अभिसरण करना चाहिए, बल्कि एक प्रतिच्छेदन बिंदु होना चाहिए।

पुनर्जागरण के उस्तादों के लिए धन्यवाद: अल्ब्रेक्ट ड्यूरर, पिएरो डेला फ्रांसेस्का, एंड्रिया मेंटेगना, लियोन बतिस्ता अल्बर्टी, आधुनिक पेंटिंग जानता है कि प्रत्यक्ष रैखिक परिप्रेक्ष्य क्या है, क्षितिज और लुप्त बिंदुओं की ऊंचाई कैसे निर्धारित करें।

और विश्व प्रसिद्ध प्रतिभा - लियोनार्डो दा विंची - ने सबसे पहले हवाई परिप्रेक्ष्य की अवधारणा का तर्क दिया। इसमें रंग में परिवर्तन, वस्तु का स्वर, इसकी विपरीत विशेषताओं में परिवर्तन (वस्तु के दूर जाने के साथ कम होना) शामिल हैं।

ऑर्थोग्राफिक प्रोजेक्शन

ऑर्थोगोनल को समानांतर प्रक्षेपण कहा जाता है, जो एक सीधी रेखा की ओर निर्देशित होता है, जो विमान के लंबवत होता है। इसके आवेदन की प्रक्रिया में, वस्तु की आकृति के आयाम अपरिवर्तित रहते हैं। अर्थात्, वस्तु बिना विकृति के प्रदर्शित होती है।

प्रक्षेपित त्रि-आयामी वस्तु, जैसे वह थी, तीन दृश्यों में विघटित होती है: बगल से, सामने से और ऊपर से। और एक ही समय में यह सब देखते हुए, आप जोड़ सकते हैंमात्रा में वस्तु कैसी दिखती है, इसका प्रतिनिधित्व। साथ ही, त्रि-आयामी छवि और द्वि-आयामी छवि दोनों में आकृति के आयाम अपरिवर्तित रहते हैं।

तिरछा प्रक्षेपण

यह प्रक्षेपण कई और उप-प्रजातियों में विभाजित है, अर्थात्:

• सममितीय दृश्य;
• डिमेट्रिक प्रोजेक्शन;
• त्रिमितीय प्रक्षेपण।

आइसोमेट्रिक के सभी 3 अक्षों (लंबाई, चौड़ाई, ऊंचाई) में विरूपण गुणांक हैं। अर्थात्, जोड़ी में लिए गए कुल्हाड़ियों के बीच के कोण 120 डिग्री के बराबर होते हैं। डिमेट्रिक एक में, 2 कुल्हाड़ियों के साथ विकृतियां बराबर होती हैं, और तीसरी अलग होती है। और त्रिमितीय प्रक्षेपण में, सभी विरूपण गुणांक (अर्थात, सभी 3 अक्षों के साथ) भिन्न होते हैं।

घूर्णन के आकार

जब एक समकोण त्रिभुज दो पैरों में से एक की धुरी पर घूमता है, तो उसकी तीसरी भुजा (कर्ण) एक नई आकृति का वर्णन करेगी जिसे शंकु कहा जाता है। और यदि आप एक आयत (वर्ग) को उसकी एक भुजा पर घुमाते हैं, तो आपको एक बेलन प्राप्त होता है। जब अर्धवृत्त घूमता है, तो एक गोला निकलेगा।

इससे यह पता चलता है कि समतल को किसी अक्ष पर घुमाने पर हमें घूर्णन के तथाकथित आंकड़े मिलते हैं।

इन आंकड़ों में घूर्णन की धुरी होती है। वे विमान में कैसे दिखते हैं यह आंखों के स्तर के सापेक्ष उनके स्थान पर निर्भर करता है। उदाहरण के लिए, एक बेलन के ऊपर और नीचे की भुजाएँ अनिवार्य रूप से वृत्त हैं। और यदि आप उन्हें एक हवाई जहाज़ में देखते हैं, तो वे दीर्घवृत्त की तरह दिखते हैं।

लेकिन काम और भी मुश्किल हो जाता है अगर, प्रदर्शित करते समयविमान पर स्थानिक आंकड़े, उनके पास एक झुका हुआ अक्ष है। इस मामले में, यह महत्वपूर्ण है कि क्रांति के निकायों की रूपरेखा उत्तरार्द्ध की धुरी से समान दूरी पर हो।

चिरोस्कोरो के बारे में थोड़ा

हवाई जहाज़ पर आकृतियों को प्रदर्शित करने में Chiaroscuro एक महत्वपूर्ण भूमिका निभाता है। क्योंकि चित्रित वस्तु का आयतन न केवल रेखाओं के कारण बनता है, बल्कि इसके किनारों पर प्रकाश और छाया के सही वितरण के कारण भी बनता है। और फिर यह द्वि-आयामी सतह के तल में काफी बड़ा दिखता है।

इस प्रकार, विमान पर आकृतियों का प्रदर्शन, उनके आकार का निर्धारण, लपट और काले धब्बों के सही ओवरले की विशेषताएं उपरोक्त विधियों के लिए काफी संभव हैं। और, सबसे महत्वपूर्ण बात, ये वास्तव में व्यवहार में सिद्ध तरीके हैं, जिनका उपयोग हमारे समय के प्रमुख विशेषज्ञों द्वारा किया जाता है।